Gauss’s Law
Gauss’s Law: Overview
This topic covers concepts, such as, Electric Flux, Area Vector, Electric Field inside the Overlapping Region of Two Oppositely Charged Spheres & Electric Field inside the Cylindrical Cavity of Uniformly Charged Cylinder etc.
Important Questions on Gauss’s Law
The electric field components due to a charge inside the cube of side are as shown:
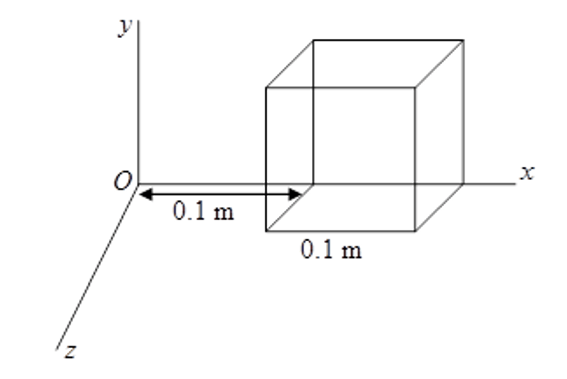
, where
.
Calculate the flux through the cube, and the charge inside the cube.
Which law is used to derive the expression for the electric field between two uniformly charged large parallel sheets with surface charge densities and respectively:
Applying Gauss theorem, the expression for the electric field intensity at a point due to an infinitely long, thin, uniformly charged straight wire is
Assertion (A): In a region of constant potential, the electric field is zero and there can be no charge inside the region.
Reason (R): According to Gauss law. charge inside the region should be zero if electric field is zero.
A solid sphere of radius carries a positive charge distributed uniformly throughout its volume. A very thin hole is drilled through it's center. A particle of mass and charge performs simple harmonic motion about the center of the sphere in this hole. The frequency of oscillation is
A hollow charged metal sphere has radius . If the potential difference between its surface and a point at a distance from the centre is, then electric field intensity at a distance is:
A cylinder of radius and length is placed in a uniform electric field parallel to the cylinder axis. The total flux for the surface of the cylinder is given by
An electron is fired directly towards a large metal plate having surface charge density . The distance from where the electron be projected so that it just fails to strike the plate is
A circular plate sheet of radius is placed in a uniform electric field of making an angle of with the field. Then find the electric flux through the sheet.
A hollow cylinder has a charge coulomb within it. If is the electric flux in units of associated with the curved surface , the flux linked with the plane surface in units of will be
A parallel plate capacitor has two square plates with equal and opposite charges. The surface charge densities on the plates are and respectively. In the region between the plates the magnitude of the electric field is
The potential (in volts) of a charge distribution is given by
for
for .
does not depend on and . If this potential is generated by a constant charge per unit volume (in units of ) which is spread over a certain region, then choose the correct statement.
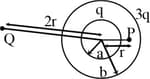
The ratio of electric field intensity at & in the shown arrangement is
A charge is placed at a distance above the centre of a square surface of side length . The electric flux through the square surface due to the charge would be?
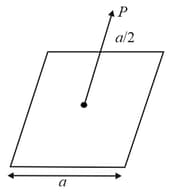
The net flux passing through the surface of an imaginary cube of edge length placed in space having a uniform volume charge density, is . The net flux passing through the surface of an imaginary sphere of radius in the same space is
Consider a uniformly charged solid cylinder of large length and radius Now consider a cylindrical surface of radius and length coaxial with cylinder and electric flux through cylindrical surface is Now consider a spherical surface of radius and one of the diameter along axis of cylinder and electric flux through spherical surface is Find to the nearest integer.
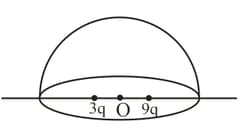
In the shown figure a hemisphere is placed and two charges and are placed symmetrically about centre Net electric flux over curved surface is given as where and are lowest possible integers then value of is :